RESEARCH
ADRIAN SCHACKER 2008-2013©
Klicken Sie auf die Abbildungen, um sie zu vergrößern.
„Gott würfelt nicht, er spielt Mondrago“ !
Die MONDRAGO – Forschung (Mondragologie) steht noch ganz am Anfang. Aber sie macht Fortschritte! Eines ihrer Ziele ist die „MONDRAGO – Formel“. MONDRAGO steckt voller mathematischer, geometrischer und ästhetischer Fragen, die noch einer zusammen hängenden Erklärung und entsprechender Analysen bedürfen.
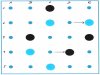
Die MONDRAGO – Formel beschreibt die Bewegung und Interaktion von 2 x 4 Spielsteinen, die nach den Regeln von MONDRAGO auf einem Spielfeld von 5 x 5 Feldern nach einem Quadrat streben, das sie sich gleichzeitig gegenseitig verhindern müssen.
1. Grundsätzliche Fragen
1.1) Das Quadrat
Die 1. Frage bei MONDRAGO ist regelmäßig die nach der Definition eines Quadrats: ein Quadrat ist ein Viereck mit vier gleichen Seiten, die durch vier rechte Winkel verbunden sind.
1.2) Anzahl der Quadrate
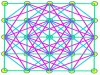Die 2. Frage, die allgemein gestellt wird, nämlich die nach der Anzahl der möglichen Quadrate (Mondragos) auf der MONDRAGO-Spielfläche, lässt sich leicht durch simples Auszählen beantworten: es sind genau 50.
30 gerade Quadrate, 10 diagonale Quadrate, 10 schräge Quadrate
Wir nennen Quadrate „gerade“, wenn ihre Seiten parallel sind mit den Grundlinien des Spielfelds.
„Diagonale“ Quadrate sind um 45 Grad gedreht.
„Schräge“ Quadrate liegen auf dem Spielfeld zwischen den „geraden“ Quadraten und den „diagonalen“ Quadraten.
1.3) Man kann die Anzahl der möglichen Quadrate natürlich auch ausrechnen (Klick auf Abb.):
ausdrucken und studieren: Anzahl aller Quadrate auf nxn Feldern. Alle Formeln und ihre Herleitung (pdf) © Dr. Bangert 2010
1.4) Das „schräge“ Quadrat. Verschiedentlich wurde bezweifelt, dass das „schräge“ Quadrat tatsächlich ein korrektes Quadrat ist. Diese Frage darf inzwischen als überholt gelten, nachdem gegen Ende des letzten Jahrhunderts der Physiker Dr. Bangert mit Hilfe der Regeln der Geometrie den Beweis dafür formulierte, dass das „schräge“ Quadrat wirklich ein korrektes Quadrat ist.
1.5) Sieg
a) Der Gegner übersieht das drohende Quadrat.
b) Der Gegner kann das drohende Quadrat nicht mehr verhindern, weil er einen Zug mehr braucht, um das fragliche Spielfeld zu besetzen.
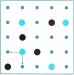c) Der Angreifer kann 2 oder mehr Quadrate gleichzeitig androhen, a) mit einem Stein, b) mit versch. Steinen, von denen der Gegner nur eines oder sogar keines verhindern kann.
Es gibt bei MONDRAGO keinen bekannten Spielzug, der von Anfang an (und unabhängig vom Gegner) direkt und zwangsläufig zum Sieg führt.
1.6) Unentschieden
Eine der Fragen, die sich sofort aufdrängt, und verschiedentlich immer noch diskutiert wird: gibt es bei MONDRAGO ein Unentschieden? Ein Unentschieden bei MONDRAGO würde (anders als bei Schach) einen unendlichen Spielverlauf bedeuten. Ist das (theoretisch) überhaupt möglich?
Ist der Spielverlauf aber endlich, wäre die noch zu klärende, grundsätzliche Frage die nach der längsten, möglichen MONDRAGO-Partie.
1.7. Patt
Wir wissen (noch) nicht, ob es bei MONDRAGO ein „Patt“ wirklich geben kann, aber wir haben schon zwei mögliche Definitionen, von denen die eine die Möglichkeit eines „MONDRAGO – Patts“ ausschließt:
a) Ein „MONDRAGO-Patt“ wäre, wenn auf Grund des Zugzwangs keine der beiden Parteien anders ziehen kann, ohne zu verlieren. Würde im Spielverlauf eine unendliche Schleife bedeuten. Bis jetzt ist kein Fall eines „Patts“ bei MONDRAGO bekannt.
b) Übernimmt man die Definition des Patts vom Schach, entspräche das „MONDRAGO – Patt“ einer Spiel-Situation, bei der ein Spieler A einen Zug machen könnte, der beim anderen Spieler B ein Mondrago-Quadrat entstehen lässt. Das kann aber nicht entstehen, indem A einen Zug macht, sondern nur, indem B selbst einen Zug macht. (V.Bangert2010)
2. Die Eröffnung
Allgemeines
Die Eröffnung und die anschließende „Eröffnungsphase“, also die ersten (mindestens 5) Züge bis zur Androhung eines Quadrats, sind ungemein wichtig für den weiteren Spielverlauf. Es empfiehlt sich, die Spielsteine gut zu verteilen. Eine umfassende und zusammenhängende Analyse der Eröffnungsphase steht noch aus.
2.1) Die umgekehrt symmetrische Anfangsstellung sorgt dafür, dass frühestens mit dem 6. Zug ein Quadrat vollendet werden kann („Sudden Death„), was vielfältige Ausgangsspositionen ermöglicht.
2.2) Anzahl der Eröffnungen
Es gibt auf jeder Seite 6 mögliche 1. Züge (Eröffnungen)
→ Die 2 schlechtesten Eröffnungen
3. Der Spielverlauf
Zugzwang (Androhung und Verhinderung) und Bifurkationen bestimmen den Mondrago – Spielverlauf.
3.1) Androhung und Verhinderung eines Quadrats
Der Mondrago – Spielverlauf dreht sich um die „Androhung“ und „Verhinderung“ eines Quadrats nach den Regeln des Spiels Mondrago. Angreifer ist, wer ein Quadrat androhen kann, Verteidiger ist, wer ein Quadrat verhindern muss.
a) Die Androhung
Wir reden von der „Androhung“ eines Quadrats, wenn ein Spieler nur noch 1 Zug vom Quadrat entfernt ist, also mit der Vollendung eines Quadrats „droht“, welches der Gegner verhindern muss, wenn er nicht verlieren will.
b) Die Verhinderung
Um ein Quadrat zu verhindern, muss der Spieler das Spielfeld besetzen, auf dem das Quadrat angedroht wird.
Der Spielverlauf ist daher wesentlich ein “Bedrohungsverlauf”. Unter “Bedrohung” verstehen wir hier die Anzahl der noch nötigen Spielzüge bis zur Vollendung eines Quadrats, d.h. bis zum Erreichen von “Mondrago“.
3.2) Der Mondrago – Phasenraum
Der „Mondrago – Phasenraum“ beschreibt den Bedrohungsverlauf einer Partie Mondrago als Diagramm. Der Phasenraum kombiniert die Anzahl der noch nötigen Spielzüge bis zur Vollendung eines Quadrats (also die “Bedrohung”) mit der fortschreitenden Zugfolge des Spiels. Auf der senkrechten y-Achse liegt die Anzahl der noch nötigen Spielzüge, auf der waagerechten x-Achse die Zugfolge. (Abb.)
3.3) Die Ebenen im Phasenraum
Der Mondrago-Phasenraum gliedert sich (von oben nach unten) in folgende 7 Ebenen:
0 = Austritt aus dem Phasenraum. Hier ist das Quadrat erreicht und das Spiel zu Ende.
1 = Noch 1 Zug bis zum Quadrat. Direkter Zugzwang.
2 = Noch 2 Züge bis zum Quadrat. Indirekter Zugzwang.
3 = Noch 3 Züge bis zum Quadrat. Indirekter Zugzwang.
4 = Noch 4 Züge bis zum Quadrat. Beginn der Wechselwirkung und damit Eintritt in den „eigentlichen“ Phasenraum (Ebenen 1 – 4), in dem die Wechselwirkung herrscht. Indirekter Zugzwang.
5 = Noch 5 Züge bis zum Quadrat.
6 = Anfangsstellung, also noch 6 Züge bis zum Quadrat (Spielbrettebene)
Der „Bedrohungsverlauf als Kurve im Mondrago – Phasenraum („Angstkurve“)
Die Erforschung des MONDRAGO – Phasenraum steht noch ganz am Anfang. Die Kurve ist um so aussagekräftiger, je besser die beteiligten Spieler sind und je mehr Züge die Partie andauert. Klick oben zum Vergrößern auf das Phasenraum-Diagramm der bisher längsten, aufgezeichneten MONDRAGO – Partie →Adrian vs. Zven(pdf)
Frage: Kann man den Phasenraum um eine oder sogar mehr Variablen erweitern?
3.4) Der Zugzwang
Aus dem Prinzip der gegenseitigen Androhung und Verhinderung entspringt bei Mondrago der Zugzwang. Angreifer ist, wer den Zugzwang ausüben kann, Verteidiger ist, wer ihm folgen muss.
Durch den Zugzwang verkoppeln sich die Teams der 2 x 4 Spielsteine. Sie treten in eine unauflösliche und dynamische Wechselwirkung, die erst mit dem vollendeten Quadrat erlischt. Innerhalb dieser Wechselbeziehung unterscheiden wir a) den direkten Zugzwang und b) den indirekten Zugzwang. Der indirekte Zugzwang betrifft die Spielzüge vor der Androhung eines Quadrats, also vor der Ausübung des direkten Zugzwangs.
a) direkter Zugzwang
Der aus der direkten Androhung eines Quadrats (also noch 1 Zug bis zum Quadrat) und dessen Verhinderung erfolgende direkte Zugzwang, der den Gegner zwingt, das fragliche Spielfeld zu besetzen, scheint, oberflächlich betrachtet, den Spielverlauf zu dominieren.
In Wahrheit aber kommt die „Bedrohung“ aus der Tiefe des Spielverlaufs, d.h. aus den Spielzügen, die der direkten Androhung des Quadrats vorausgehen.
b) indirekter Zugzwang
Erfahrene Mondrago – Spieler wissen daher, dass es nicht ausreicht, dem Zugzwang folgend, die angedrohten Quadrate zu verhindern. Sie versuchen, mindestens 2 Züge voraus blickend, schon die Androhung eines Quadrats zu verhindern, indem sie das fragliche Spielfeld, von dem die Androhung ausgehen könnte, besetzen. Dies nennen wir den „indirekten“ Zugzwang.
Nun ließe es sich denken, dass man das nächst mögliche Quadrat nur richtig vorausschauen müsste, sozusagen immer nur „richtig“ ziehen müsste, um als Angreifer die Bedrohung konstant bis zur Vollendung des Quadrats aufrecht halten zu können. Das würde bedeuten, dass der, der anfängt, immer gewinnt, weil er immer mindestens 1 Zug vorne bleibt. Umgekehrt würde „richtig“ ziehen aber bedeuten, dass der Verteidiger dieses Quadrat immer verhindern kann, was auf ein Unentschieden, d.h. einen unendlichen Spielverlauf, hinauslaufen würde.
Beide Vorstellungen schließen sich gegenseitig aus. Sie gehen von einem linearen Spielverlauf aus. Wäre es so, gäbe es aber kein „Spiel“. In Wahrheit verändern sich mit jedem Zug die Abstände zu den jeweiligen Quadraten für beide Spieler verschieden, was im Mondrago – Phasenraum als „Bedrohungsverlauf“ ja auch sichtbar wird. Diesen Effekt des gegenseitigen Zugzwangs nennen wir die „Mondrago – Wechselwirkung“.
Es ist so: der Angreifer kann nicht immer nur angreifen. Er muss ja auch die Möglichkeit des Gegners kalkulieren, selber ein Quadrat bilden zu können, dass dieser vielleicht sogar schneller erreichen kann, welches er, solange der Zugabstand zum nächst mögl. Quadrat zwischen beiden Spielern gleich ist, und solange er den Zugabstand nicht verringern kann, vorausschauend verhindern muss. So ist er gleichzeitig Verteidiger. Das ist eben ist der „indirekte“ Zugzwang. Die Entscheidung fällt also in der Tiefe des Spielverlaufs, in den Zügen vor der Bildung des Quadrats. Dort dreht sich (oft unbemerkt) das Spiel. Der Angreifer wird zum Verteidiger, der Verteidiger wird zum Angreifer.
3.5) Die Mondrago – Wechselwirkung
Allgemeines
„Wechselwirkungen“ sind Rückkopplungen. Sie verhalten sich wie Frage und Antwort, wobei die Antwort stets zur neuen Frage wird und die Frage wieder zur Antwort.
Die „Mondrago – Wechselwirkung“ beruht auf zwei gegensätzlichen Prinzipien, die sich ausschließen und sich gleichzeitig gegenseitig bedingen: der Bildung eines Quadrats und seiner Verhinderung. Sie betrifft ausschließlich die Bildung und Verhinderung von Quadraten mit jeweils 4 Spielsteinen auf einer Spielfläche von 5*5 Feldern nach den Regeln des Spiels Mondrago. Ihre mathematische Formulierung („Mondrago – Formel“) steht noch aus.
Zu beachten ist, dass die Mondrago – Wechselwirkung bei näherer Betrachtung sich aus 2 Interaktionen zusammensetzt: a) Die Wechselwirkung zwischen beiden Parteien über den gegenseitigen Zugzwang („Große Wechselwirkung“), und b) die Wechselwirkung innerhalb der 4 Spielsteine einer Partei („Kleine Wechselwirkung“).
a) Große Wechselwirkung
Die Mondrago – Wechselwirkung entsteht und entfaltet sich im Spielverlauf über den gegenseitigen Zugzwang, der die „Androhung“ und „Verhinderung“ eines Quadrats bis zur Vollendung des Quadrats verbindet und den Spielverlauf, den wir ja als „Bedrohungsverlauf“ definiert hatten, (Spielzug um Spielzug) in sich selbst zurückkoppelt. Diese Rückkopplung bewirkt, dass sich das Spiel unversehens drehen kann, indem sie die Entfernung zum nächst mögl. Quadrat für beide Spieler von Spielzug zu Spielzug unterschiedlich verändern kann.
b) Kleine Wechselwirkung
Das liegt daran, dass auch die 4 Spielsteine innerhalb der Spielfläche eine eigene Interaktion haben. Einerseits drehen sie sich um das eigene Quadrat, das sie bilden wollen, andererseits müssen sie (als Ganzes) auf das möglicherweise sich gleichzeitig bildende, d.h. „drohende“ Quadrat des Gegners reagieren, was wiederum auf die Interaktion zwischen den Spielsteinen zurückwirkt.
Diese Interaktion ist aus den Bedingungen (Spielregel) gegeben, weil jeder Spieler nur die Mindestzahl von 4 Spielsteinen für die 4 Ecken eines Quadrats hat, die der gleichen Regel unterliegen (pro Zug ein Feld), jeder Spielstein also zählt und gleich wichtig ist.
Sichtbar wird die Mondrago – Wechselwirkung auch in den vielfältigen geometrischen Konstellationen, die sie auf dem Spielfeld generiert.
Die Mondrago – Wechselwirkung ist Ausdruck der einzigartigen Ganzheitlichkeit des Spiels Mondrago.
3.6) Bifurkationen
Selbst bei konsequentem Angreifen und Verhindern getreu des gegenseitigen Zugzwangs ergeben sich immer wieder Konstellationen, bei denen ein Spieler z.B. 2 Quadrate mit derselben Zugzahl erreichen kann, von denen der Gegner aber nur eines verhindern kann. Auch hier kann sich das Spiel drehen. Hier spätestens gabelt sich der vom Zugzwang abhängige Spielverlauf, was wir eine „Bifurkation“ nennen.
Die Bifurkationen, also die Gabelungen des Spielverlaufs, sind Teil der Wechselwirkung und neben der Entfernung zum nächst mögl. Quadrat der 2. entscheidende Faktor im Mondrago – Spielverlauf. Es sind die Bifurkationen (und Trifurkationen), die den Spielverlauf so schwer berechnen lassen, und, wie wir glauben, ein Unentschieden unmöglich machen. Sie können über Sieg oder Niederlage entscheiden. Auch dieses Prinzip herrscht auf allen Ebenen des Phasenraums, also den Zügen vor der Bildung eines Quadrats. Die Bifurkationen (und noch mehr die selteneren Trifurkationen) liegen zwar auch innerhalb der Logik des Spiels, also der Wechselwirkung, sind aber gewissermaßen die Freiheit der Wahl in dem ansonsten über den Zugzwang so streng geregelten Mondrago – Spielverlauf.
a) Welche Bifurkationen gibt es?
1. Die Wahl zwischen versch. Spielfeldern für einen und denselben Spielstein.
2. Die Wahl zwischen versch. Spielsteinen für dasselbe Spielfeld.
3. Die Wahl zwischen versch. Spielsteinen und versch. Spielfeldern.
4. Die Wahl zwischen versch. Quadraten mit einem Spielstein.
5. Die Wahl zwischen versch. Quadraten mit versch. Spielsteinen.
6. Die Wahl zwischen 2 Ecken desselben Quadrats mit 2 Spielsteinen.
7. Die Wahl zwischen der direkten Androhung oder indirekten Androhung eines Quadrats. (Manchmal kann es besser sein auf die direkte Androhung zu verzichten, um eine bessere Gesamtposition zu erreichen)
8. Die Wahl zwischen der direkten Verhinderung des Quadrats oder der Verhinderung der Androhung eines Quadrats.
Frage: Welche Bifurkationen gibt es noch?
3.7) Trifurkationen
Was über die Bifurkationen gesagt wurde, gilt in verstärktem Maße auch für die „Trifurkationen“, also die „Dreigabelung“ des Mondrago – Spielverlaufs, wenn z.B. 3 Spielsteine zur Verfügung stehen, um ein Quadrat zu verhindern, oder wenn sogar 3 Quadrate angedroht werden können.
4. Das Mondrago – Spielfeld
4.1) Das Spielfeld ist die Basis-Ebene. Auf ihr ist der Spielstein gesetzt. Daher müssen wir die 25 Spielfelder des Spielfelds genauer betrachten, da die Spielfelder als Ausgangspunkte möglicher Quadrate auf dem begrenzten MONDRAGO – Spielfeld ja nur bestimmte Quadrate in einer bestimmten Anzahl zulassen. Wir nennen dies die „Valenz“ eines Spielfelds.
4.2) Die Valenz eines einzelnen Spielfelds ist abhängig von seiner Lage auf dem Gesamtspielfeld. In dieser Hinsicht sind die Spielfelder nichtallegleich. Sie haben verschiedene Valenzen. (Klick links aufs Bild. Die Zahlen auf den Spielfeldern bezeichnen die Anzahl ihrer Valenzen).
4.3) Die Summe aller Valenzen beträgt 200, was die Zahl der auf dem Spielfeld möglichen Quadrate vervierfacht.
4.4) 5 der MONDRAGO – Spielfelder erlauben keine schrägen Quadrate. Es sind die 4 Eckfelder der MONDRAGO – Spielfläche und das Feld in der Spielfeldmitte. Die Eckfelder haben die wenigsten Valenzen (4), die Spielfeldmitte die meisten Valenzen (12).
5. Die Spielfeldmitte
Das Spielfeld in der MONDRAGO – Spielfeldmitte ist das problematischste aller MONDRAGO – Spielfelder. Als Ausgangspunkt für die Bildung eines Quadrats ist es im Normalfall weniger geeignet, obwohl es die meisten Valenzen hat. Dieser scheinbare Widerspruch erklärt sich aus dem Umstand, dass das Mittelfeld nur die kleineren der geraden und diagonalen Quadrate zulässt, von denen es auf der MONDRAGO-Spielfläche zahlenmässig am meisten gibt, aber z.B. keine schrägen Quadrate.
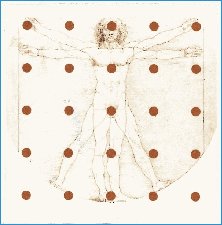
5.1) Problematisch ist die Spielfeldmitte vor allem aber wegen ihrer strategischen Bedeutung. Man muss sich klarmachen, dass jeder der 4 Spielsteine im Idealfall nur ein Viertel des Spielfelds erreichen und abdecken kann. (Abb. links) Wer daher (durch Zugzwang) das Mittelfeld besetzen muss, hat den strategischen Nachteil, dass er nun einen Teil seines Einzugsgebiets nicht mehr ausreichend abdecken kann. Er gerät in die Defensive. In diesem frei gewordenen Raum können sich für den Angreifer Möglichkeiten zur Bildung eines Quadrats eröffnen, das der Gegner nicht mehr verhindern kann. Eine der Strategien ist es daher, den Gegner durch Zugzwang auf das Mittelfeld und damit in die Defensive zu zwingen. (Siehe Musterspielzug 1) Erfahrene MONDRAGO-Spieler haben darauf stets ein besonderes Augenmerk.
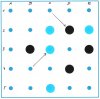
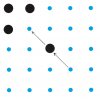5.2) Eine gewisse Ausnahme bildet die sogenannte „Hannifan-Variante„, (sprich: Hannifän), bei der das Mittelfeld vom Angreifer offensiv als „Passage“ benutzt wird. um etwa eines der kleinen Quadrate in einer der Spielfeldecken anzudrohen. Der „echte Hannifan“ (Abb.) führt mit dem 6. Zug zum vorzeitigen Ende der Partie („Sudden Death“). Erfolg oder Misserfolg hängen vom Überraschungseffekt und von der jeweiligen Stellung des Gegners ab.
Bis jetzt kennen wir 3 weitere Varianten der Hannifan-Variante:
→Variante 1 der Hannifan-Variante (4 Züge) PDF
→Variante 2 der Hannifan-Variante (8 Züge) PDF
→Variante 3 der Hannifan-Variante (6 Züge) PDF
5.3) Die Hannifan-Variante als Verteidigungs-Variante:
→Der Hannifan als Widersacher des Fiesen Sven (PDF)
6. MONDRAGO-MUSTERSPIELZUG 1
Diese Zugfolge ist gut geeignet, die Bedeutung der „Bifurkation“ und der Spielfeldmitte für den Spielverlauf in wenigen Spielzügen darzustellen. Die Spielvariante A führt zwangsläufig zu einem MONDRAGO für Schwarz nach 4 Zügen. Der Verlauf der Spielvariante B bleibt dagegen nach 4 Spielzügen noch offen.
6.1) Spielvariante A
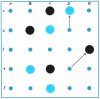
1. Zug: D4 – E3; D2 – D1;Schwarz droht ein schräges Quadrat auf D1 an. Blau hat 2 Steine (auf C2 bzw. D2) zur Verfügung, um dem Zugzwang zu folgen und das drohende Quadrat auf D1 zu verhindern. (Bifurkation) Blau wählt den Stein auf D2.Dieser Ast des Spielverlaufs endet nach 4 Spielzügen mit der zwangsläufigen Niederlage von Blau.
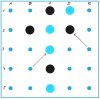
2. Zug: E3 – D2; A4 – C3; Schwarz zieht auf das von Blau geräumte D2 und droht ein kleines, diagonales Quadrat auf C3, dem Mittelfeld, an.Blau muss, dem Zugzwang folgend, auf die Mitte.
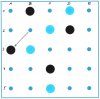
3. Zug: C1 – B1; C3 – B3; Schwarz droht ein schräges Quadrat auf A3 an, welches Blau nicht mehr verhindern kann. Blau braucht einen Zug mehr, um A3 zu besetzen.
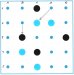
4. Zug: B2 – A3; Schwarz vollendet das schräge Quadrat auf A3 und sagt „MONDRAGO“.
6.2) Spielvariante B
1. Zug: D4 – E3; C2 – D1; Schwarz zieht wie in Variante A und droht ein schräges Quadrat auf D1 an. Blau wählt nun den anderen Stein, der ihm zur Verfügung steht, (auf C2), um das Quadrat zu verhindern (Bifurkation)
2. Zug: B2 – C2; Schwarz kann (im Unterschied zur Variante A) kein weiteres Quadrat mehr androhen und braucht einen Zwischenzug. Für Blau ergeben sich daraus verschiedene Optionen. Wir wählen D1 – C2.
3. Zug: C1 – D2; Schwarz droht ein schräges Quadrat auf E2 an. Blau verhindert mit D2 – E2
4. Zug: C1 – D2; Schwarz droht ein kleines, diagonales Quadrat auf C3, dem Mittelfeld, an. Blau hat zwei Steine, um dieses Quadrat zu verhindern (auf B4 und C2). (weitere Bifurkation). Blau wählt den Stein auf B4: B4 – C3
Im Unterschied zur Variante A ist die Partie in der Variante B nach 4 Zügen noch offen.
Wird fortgesetzt.
Letzter Stand: März 2013