Es gibt kein MONDRAGO – Patt
November 13, 2010 | Blogroll • Research • Volker | 1 Comment
Gibt es ein Mondrago-Patt?
Nein, es gibt kein Mondrago-Patt.
Im Schach entsteht eine Patt-Situation, wenn ein Spieler keinen Zug mehr machen kann, ohne sich dabei selbst in eine Schach-Matt-Situation zu bringen.
Meistens geschieht das, wenn einer der Spieler nur noch einen König hat, der nur noch in eine Schach-Matt-Situation ziehen kann. Das Spiel gilt dann als unentschieden.
Es gibt beim Mondrago-Spiel keine vergleichbare Situation. Das würde ja erfordern, dass eine Situation entsteht, bei der ein Spieler A einen Zug machen kann, der beim anderen Spieler B ein Mondrago-Quadrat entstehen lässt. Das kann aber nicht entstehen, indem A einen Zug macht, sondern nur, indem B selbst einen Zug macht.
Mit Gruß, Volker Bangert, 11.11.2010
Gott, die Welt und MONDRAGO
Mai 18, 2010 | Blogroll • Mondrago - Bar Berlin • Volker | Leave a Comment
Der Mondrago-Abend war ja sehr gut besucht, bei echt guter Atmosphäre.
„Gott würfelt nicht, er spielt Mondrago!“.
Herzlich Volker
Anzahl aller Quadrate auf n*n Feldern
März 18, 2010 | Research • Volker | Leave a Comment
Hallo Quadratköpfe, Volker hat es geschafft! Alle Formeln und ihre systematische Herleitung zur Anzahl mögl. Quadrate auf n*n Spielfeldern (bei MONDRAGO n=5), einschließlich der Differenzen der daraus resultierenden Zahlenfolgen, steht nun für alle mathematisch Interessierten zur Verfügung. Die Zahlenfolgen werden als Tabellen und als Kurven gezeigt! Big stuff!
Ausdrucken und studieren: Anzahl aller Quadrate auf nxn Feldern. Alle Formeln und ihre Herleitung (pdf) © Dr. Bangert 2010
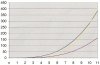Man sieht, die Kurve der schrägen Quadrate schneidet die Kurve der diagonalen Quadrate genau bei n = 5, was der Tatsache entspricht, dass es auf einem MONDRAGO – Spielfeld (5*5) gleich viele diagonale wie schräge Quadrate gibt, nämlich 10. Danach nehmen die diagonalen Quadrate im Verhältnis zu den schrägen immer mehr ab.
Die Kurve der schrägen Quadrate hat zwei Schnittpunkte: Zwischen n=10 und n=11 schneidet sie die Kurve der geraden Quadrate. Ab einem Spielfeld von n=11 gibt es also mehr schräge als gerade Quadrate.
Die Anzahl diagonaler Quadrate ist immer kleiner als die Anzahl der geraden Quadrate.
Die Differenzen in den Zahlenfolgen geben Einblicke in das innere Verhältnis der Anzahl der Quadrate, z.B. ergibt die 1. Differenz der Anzahl der geraden Quadrate selber die fortlaufende Folge der Quadratzahlen n*n. →Research
Die Anzahl möglicher Quadrate
Januar 23, 2010 | Blogroll • Research • Volker | Leave a Comment
Zum Glück hat das MONDRAGO – Spielfeld nur 5 x 5 Felder, denn auf einem Spielfeld von 101 x 101 Feldern würde die Anzahl der möglichen Quadrate schon die 1 Million überschreiten.
Die von unserer Grundlagen-Forschung gefundene math. Formel (Klick auf Abb.) erlaubt die Berechnung der Anzahl mögl. Quadrate auf n x n Spielfeldern. Ist die Formel nicht wunderbar? Sie enthält die Summe aller geraden, diagonalen und schrägen Quadrate. Sie stimmt für alle ganzen Zahlen. Es lohnt sich, sie genauer zu betrachten. Wenn ihr mehr wissen wollt: →Research
PS: Wenn ihr wissen wollt, wie viele mögliche Quadrate es bei MONDRAGO gibt, könnt ihr die Formel benutzen, indem ihr für n = 5 einsetzt.
Grundlagenforschung
Januar 9, 2010 | Blogroll • Research • Volker | Leave a Comment
MONDRAGO – Spieler wissen schon seit Urzeiten, dass es auf dem Mondrago- Spielfeld n*n, (wobei n=5), genau 50 mögl. Quadrate, (Mondragos) gibt: 30 gerade, 10 diagonale und 10 schräge Mondragos. Aufgepasst! Volker hat nun für die Anzahl der Mondragos auf n*n Spielfeldern das allgemeine Bildungsgesetz gefunden:
mn (gesamt) = Gesamtzahl aller möglichen Mondragos auf einem Spielbrett mit n*n Feldern.
mn (gesamt) = mn (gerade) + mn (schräg) + mn (diagonal)
1. Gerade Mondragos: mn (gerade) = (n-1)2 + (n-2)2 +(n-3)2 …… + (n-(n-1))2
2. Schräge Mondragos: mn(schräg) = 2*(n-3)2 + 2*(n-4)2 + 2*(n-5)2 +…2*(n-(n-1))2
3. Diagonale Mondragos: mn(diagonal für ungerades n) = (n-2)2 + (n-4)2 +(n-6)2 …+ (n-(n-1))2
mn (diagonal für gerades n) = (n-2)2 + (n-4)2 +(n-6)2 …… + (n-(n-2))2
4. Alle Mondragos: mn(gesamt für ungerades n) =1*(n-1)2 + 2*(n-2)2 +3*(n-3)2 + 4*(n-4)2 + 3*(n-5)2 +4*(n-6)2 + 3*(n-7)2 +4*(n-8)2 …… + 4*(n-(n-1))2
mn (gesamt für gerades n) = 1*(n-1)2 + 2*(n-2)2 +3*(n-3)2 + 4*(n-4)2 + 3*(n-5)2 +4*(n-6)2 + 3*(n-7)2 +4*(n-8)2 …… + 3*(n-(n-1))2
n = immer ganze Zahlen